Как определить общее сопротивление резистора в электрической цепи?
Если не использовать специальные технические решения по увеличению проводимости сопротивление имеют все проводники электротока. Даже провод может оказаться не пригодным при большой силе тока и его придётся заменять, например, медной шиной. Определить величины тока в источнике питания, и в нагрузках позволяет расчет сопротивления электрической цепи.
Два вида соединений элементов может быть в электрической схеме:
- последовательное;
- параллельное.
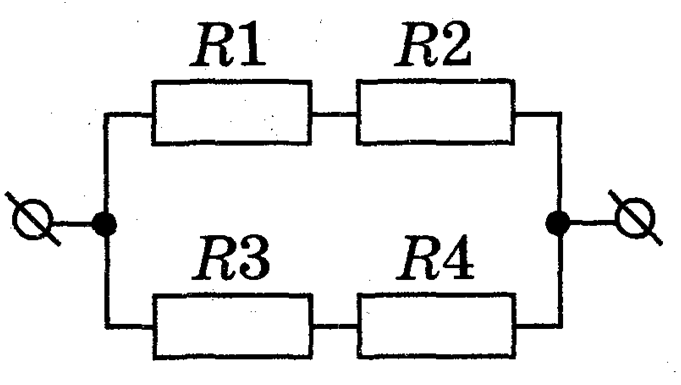
На изображении выше показаны четыре нагрузки. Из них R1 и R2 соединены последовательно, так же, как и нагрузка R3 c R4. Но в этой схеме есть и параллельное соединение: R1и R2 параллельны R3 и R4.
В любых электрических цепях элемент с функциями сопротивления именуется как «резистор». Если в электрической схеме n резисторов соединены последовательно величины их сопротивлений суммируются. Следовательно, общее сопротивление электрической цепи Rобщ.
- Rобщ.=R1+R2+…+Rn
При параллельном соединении n резисторов для Rобщ. справедливо выражение
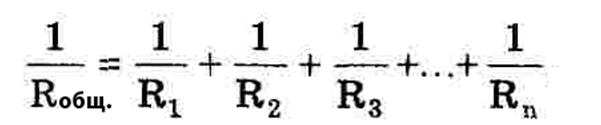
Сколько бы ни было резисторов в электрической схеме их можно заменить одним элементом эквивалентного сопротивления и определить ток в этом элементе по закону Ома. Для этого шаг за шагом выполняется замена нескольких резисторов одним в соответствии с их соединением – параллельным или последовательным. На примере первого изображения с резисторами R1, R2, R3 и R4 получится следующее. Сначала заменяем R1 и R2 на R5:
- R5= R1+R2
Затем заменяем R3 и R4 на R6:
- R6=R3+ R4
В результате получается новая эквивалентная схема из R5 и R6, соединённых параллельно
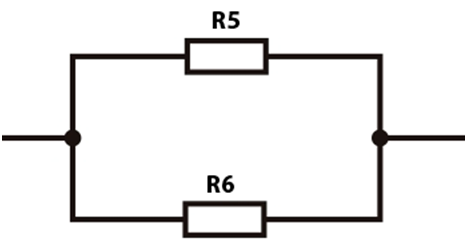
А конечный результат определить легко:
- 1/Rобщ.=1/R5 + 1/R6,
- Rобщ.=R5*R6/(R5+R6)
В том случае, когда не удаётся сразу сделать замену нескольких элементов одним, как например, на схеме, показанной ниже
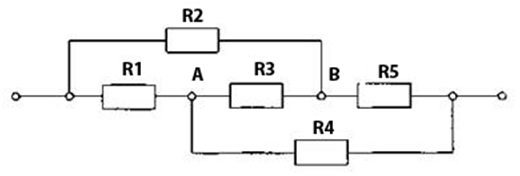
следует сделать её анализ. В приведенном изображении, очевидно, что сумма токов в нагрузках R1 и R2 равна сумме токов в нагрузках R4 и R5. Следовательно, потенциалы точек А и В равны, и могут быть объединены. Ток через нагрузку R3 не течёт. Получаются такие соединения
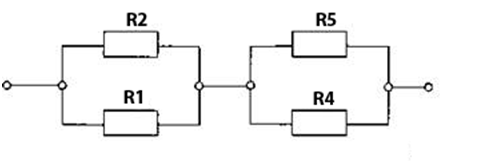
Эти соединения нагрузок легко преобразуется сначала в два последовательно соединённых элемента, а затем в одно эквивалентное сопротивление. Для более сложных и разветвлённых цепей применяется такой же метод.